오차가 쉽게 발생하는 센서를 사용하여 뉴턴 역학을 따르는 물체를 추적하는 전형적인 예를 살펴 보자. 물체의 위치를 물체의 속도와 가속도에 대한 함수로 보는 뉴턴 운동법칙 Newton's laws of motion에 따라 시계열을 생성한다.
이 때 물체의 움직임은 계속성을 갖지만, 측정이 이산적으로 분리된다고 가정해보자. 우선 가속도에 대한 계열을 정하고, 위치와 속도는 0에서 시작한다. 또한 물리적으로 비현실 적이지만 각 시간 단계에서 각 시간단계의 시작점에서 순간 가속도가 변하고 다시변하기 전까지는 지속적인 값을 가진다고 가정 하자.
# 코드로 표현한 칼만 필터
## 로켓은 시간 단계를 100번 거칩니다.
ts.length <- 100
## 가속도가 움직임을 주도한다.
a <- rep(0.5, ts.length)
## 위치와 속도는 0에서 시작한다.
x <- rep(0, ts.length)
v <- rep(0, ts.length)
for (ts in 2:ts.length){
x[ts] <- v[ts -1] *2 + x[ts-1] + 1/2 * a[ts-1] ^2
x[ts] <- x[ts] +rnorm(1, sd =20) ## 확률적 요소
v[ts] <- v[ts -1] +2 * a[ts-1]
}뉴턴 운동 법칙을 잘 모르거나 기억나지 않는다면 값을 있는 그대로 받아 들여도 좋다. 다만 해당 개념에 익숙해도록 노력하는 것이 우리의 목적(x[ts] 및 v[ts]의 계산)을 좀 더 분명히 이해하는데 도움을 준다.
그래프를 그려보면 코드로 구조화 하여 만든 가속도에 따른 움직임을 볼 수 있다.
par(mfrow = c(3,1))
plot(x, main = "Posision", type = 'l')
plot(v, main = "Velocity", type = 'l')
plot(a, main = "Acceleration", type = 'l') |
| 로켓의 위치, 속도, 가속도에 대한 그래프 |
위 그림은 선형으로 증가하는 속도(중단 그래프)에 영향을 주는 일정한 가속도(하단 그래프)가 위로 솟구치는 볼록 모양의 그래프(상단 그래프)를 만들어 냄을 알 수 있다. 이 그래프 모양이 익숙치 않다면 단순히 있는 그대로 받아들이거나 물리학 입문서를 참고하는 걸 권장 한다.
모든 상태가 이 세 변수로 묘사 된다고 가정 하자. 하지만 우리에게 가용한 데이터는 오직 노이즈한 센서로 부터 얻을 수 있는 물체의 위치 뿐이다. 다음 코드는 측정된 값이 실제위치와 어떤 관계를 갖는지 에 대한 그리프를 그린다. 여기서 변수 x가 센서를 의미 한다.
par(mfrow = c(1,1))
z <- x + rnorm(ts.length, sd =300)
plot(x, ylim = range(c(x,z)))
lines(z, col ="2") |
| 참 위치(원)와 오차가 있는 측정(선)간의 관계를 보여준다. 상태 천이 공식에 넣은 노이즈로 인해 위치 x가 완벽한 볼록을 반영하지 않는 다는 사실에 유의해야 한다. |
칼만 필터를 적용할 차례이다. 우선 앞부분에서 다룬 내용과 도출된 식을 반영할수 있는 일반적인 함수 코드로 작성 한다.
https://rdmkyg.blogspot.com/2021/08/blog-post_27.html
## 칼만필터 적용
kalman.motion <- function( z, Q, R, A, H){
dimState = dim(Q)[1]
xhatminus <- array(rep(0, ts.length *dimState), c(ts.length, dimState))
xhat <- array(rep(0, ts.length * dimState), c(ts.length, dimState))
Pminus <- array(rep(0, ts.length * dimState * dimState),
c(ts.length, dimState, dimState))
P <- array(rep(0, ts.length * dimState * dimState),
c(ts.length, dimState, dimState))
K <- array(rep(0, ts.length * dimState),
c(ts.length, dimState)) # 칼만 이득 K
# 초기 추축 = 모든 지표는 0으로 시작한다.
xhat[1, 0] <- rep(0, dimState)
P[1, , ] <- diag(dimState)
# 시간 갱신
for(k in 2:ts.length){
# 예측
xhatminus[k, ] <- A %*% matrix(xhat[k-1,]) # %*% : 행렬 곱셈 연산자
Pminus[k, , ] <- A %*% P[k-1, ,] %*% t(A) + Q
# 필터링
K[k, ] <- Pminus[k, , ] %*% H %*% # 대문자 K와 소문자 K를 헤갈리면 안된다.
solve( t(H) %*% Pminus[k, , ] %*% H + R )
xhat[k, ] <- xhatminus[k, ] + K[k, ] %*%
(z[k] - t(H) %*% xhatminus[k, ])
P[k, , ] <- (diag(dimState) - K[k, ] %*% t(H)) %*% Pminus[k, , ]
}
## 예측과 평활화 된 값 모두를 반환 한다.
return(list(xhat = xhat, xhatminus = xhatminus))
}
# 노이스 파라미터
R <- 10^2 ## 측정분산 - 이 값은 측정두고에 대해 알려진,
## 물리적 한계에 따라 설정 되어야 한다.
## x에 더해진 노이즈와 일관성 있게 설정 합니다.
Q <- 10 ## 과정의 분산 - 일반적으로 성능의 최대화를 위해서
## 조정되어야 하는 하이퍼 파라미터로 취급 된다.
# 동적 파라미터
A <- matrix(1) ## y_t = A x_t-1(사전 x가 나중 x에 얼마나 영향을 미치는지)
H <- matrix(1) ## y_t = H * x_t(상태를 측정으로 변환)
## 칼만 필터 방법으로 데이터를 넣고 돌린다.
xhat <- kalman.motion(z, diag(1) * Q, R, A, H)[[1]]
xhatminus <- kalman.motion(z, diag(1) * Q, R, A, H)[[2]]위의 함수를 적용하여, 로켓의 위치만을 측정 가능하게 만들어 준다. (즉, 속도와 가속도는 포함 하지 않는다.)
아래와 같이 참된 위치, 측정된위치, 추정된 위치에 대한 그래프를 그린다.
## visualization
plot(z, ylim = range(c(x, z)), type = 'l',
col = "black", lwd = 2)
lines(x, col = "red", lwd = 2, lty = 2)
lines(xhat, col = "orange", lwd = 1, lty = 3)
lines(xhatminus, col = "blue", lwd = 1, lty = 4)
legend("topleft",
legend = c("Measured", "Actual", "Filtered", "Forecast"),
col = c("black", "red", "orange", "blue"),
lty = 1:4) 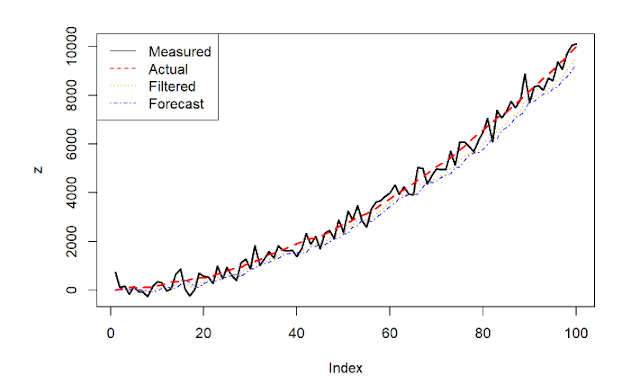 |
| 측정위치, 실제/참 위치, 필터링 된 추정된 위치(즉, 시간 t에서의 위치와 시간 t의 측정을 결합한 최상의 추정), 예측된 위치(즉, 시간 t를 포함 하지 않은 t-1까지의 측정에 알고 있는 실스템 역동성을 더한 것을 시간 t의 위치 결합한 최상의 추정)와 같은 여러 수치를 표현 한다. |
칼만 필터는 측정 오차에서 많은 노이즈를 제거 한다. 제거하는 정도는 측정 오차의 파라미터 R에 값에 따라 달라진다. 이 값은 필터가 과거 대비 가장 최근의 데이터가 얼마나 큰 가중치를 부여하는지를 반영한다. 필터는 꽤 만족스러운 예측을 만들어 낸다. 특히 예측과 실제 데이터 사이에 시간차가 없다는 사실에 주목해야 한다. 즉 직전 값에만 의존해서 현재 값을 예측 했다는 것이다.
칼만 필터의 한 가지 대단한 이점은 재귀성 recursive에 있다. 과정이 반복될 때 마다 모든 데이터를 살펴볼 필요가 없다는 의미이다. 그 대신 각 시간 단계에서, 그 이전 시간들로 부터의 모든 정보가 최근 상태, 공분산 추정이라는 몇 개의 파라미터로서 최선의 방법으로 결합되어 제공 된다.
이러한 '요약 통계' 를 사용하여 지능적인 방식으로 갱신을 수행 한다는 점이 칼만 필터의 장점이다. 이는 계산 자원 및 소요 시간이 매우 중요한 실세계의 애플리케이션에 서 칼만 필터를 매우 유용하게 해준다. 또한 여러 실세계 시스템의 역동성이 상대적으로 마르크프 연쇄 과정을 가지고, 시스템을 표현하는 함수에도 어느 정도 측정 오차가 포함 된다는 사실과 일치 하기도 하다. 실 세계를 잘 반영한다는 의미이다.
칼만 필터의 여러가지 유용한 확장이 있다. 예를 들면 칼만필터의 한 가지 주된 용도는 평활화에 적용하는 것이다. 즉 시간 t에서의 참 상태 추정에 시간 t의 전후 데이터를 모두 사용하여 최선의 추정을 한다는 것이다. 수학 및 코드는 이미 제시된 것과 유사하다. 또한 비선형적 역동성을 가진 데이터에 칼만 필터를 적용하는 확장 칼만필터 extended Kalman filter(EKF)와도 유사하다. 이를 구현하는 것은 비교적 간단한 작업이지만, 이를 지원하는 R과 파이썬의 여러 패키지가 존재 하므로 쉽게 접근 할 수도 있다.
시계열 길이에 대한 칼만 필터의 시간 복잡도 O(T) 지만, 상태의 차원 d에 대해서는 $O(d^2)$ 이다. 따라서 간단한 상태만으로도 결과가 괜찮다면, 지나치게 많은 상태를 지정하지 않는 것이 좋다. 그러나 시계열에 대한 이러한 선형성 덕분에 시계열 상태공간 모델링에서 다른 필터보다 칼만 필터를 훨신 더 많이 사용했다.







댓글 없음:
댓글 쓰기