분산과 표준편차 정말 많이 쓰이는 것이다. 분산과 표준편차는 주식시장에서 가장 많이 쓰이는 단어이다. 수익의 변화율을 분산이라고 하는데, 즉 변화율이 높다는 것은 분산과 표준편차가 크다는 것이다. 분산과 표준편차를 기반으로 포트폴리오 이론이 정립되었다.
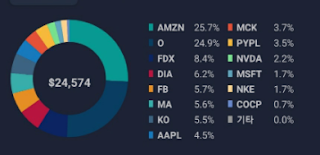 |
| 자산구성 분산과 표준편차 |
분산과 표준편차
확률변수 X의 기대값(모평균)을 μ = E(X) 라 할 때, X와 모평균의 차이를 제곱한 것의 기대값 $E(X - μ)^2 $을 X의 분산 (variance) 또는 모분산 (population variance) 이라고도 한다.
다음 식은 V(X) 또는 $σ^2$을 나타낸다.
$$ σ^2 = V(X) = E((X-μ)^2), μ = E(X) $$
분산의 제곱근인
$$ σ = \sqrt{ E((X-μ)^2) } $$
을 표준편차(standard deviation)이라고 한다. σ(시그마)는 알파벳 s 에 해당하는 그리스 문자이다. SD 라고 쓸 때도 있다.
X에서 꺼낸 n개의 $X_1, X_2, \cdot\cdot\cdot , X_n$은 다음 식을 만족한다.
$$ E((X_1- μ)^2 + (X_2 - μ)^2 + \cdot\cdot\cdot + (X_n - μ^2) = nσ^2 $$
하지만 모평균 (모집단 평균값) μ는 실제로 알 수 없는 값이다. μ 대신 표본평균 $ \bar{X} = { 1\over n } (X_1 + X_2 + \cdot\cdot\cdot + X_n)$ 의 값을 사용하면 위 식의 왼쪽 변의 값이 작아 지며 다음 식이 성립 된다.
$$ s^2 = { 1 \over n-1 }((X_1 - (\bar{X}))^2 +(X_2 -(\bar{X}))^2 + \cdot\cdot\cdot + (X_n - (\bar{X}))^2 $$
그러면 $ S^2$의 기대값은 모분산과 일치 한다.
$$ E(s^2) = σ^2$$
여기에서 이야기 하는 요점은 표준분산 n 으로 나누는 방법이 아니라, n-1로 나누는 것이다.
※ 통계학 교과서적인 내용
표본분산 계산에서 표본의 크기를 n-1로 나누는 것은 n으로 나누는 것에 비해서 일반적으로 더 정확한 추정이 가능 하기 때문이다. 여기서 n-1을 자유도(degree of freedom)라고 하고 그 직관적인 의미는 다음과 같다. 자료로 부터 평균까지의 편차합을 구하면 항상 0 이 되어서 n -1개 자료의 편차만 알면 나머지 하나의 편차를 알 수 있게 된다. 따라서 전체 n개의 자료값 중에서 n-1개의 자료값 만이 자유롭게 변화 할 수 있다는 의미에서 자유도 라고 한다.
위에 있는 의미를 이해하기 매우 어려우니 R을 이용한 간단한 수식으로 실험해 보자
> # 모분산 추정 예제
>
x = 1:5
>
var(x)
[1] 2.5
>
> # 아무 숫자나 하나를 빼보자
>
var(c(2, 3, 4, 5))
[1] 1.666667
>
var(c(1, 3, 4, 5))
[1] 2.916667
>
var(c(1, 2, 4, 5))
[1] 3.333333
>
var(c(1, 2, 3, 5))
[1] 2.916667
>
var(c(1, 2, 3, 4))
[1] 1.666667
>
>
mean(c(1.666667, 2.916667, 3.333333, 2.916667, 1.666667))
[1] 2.5
위의 R예제를 보면, 한 개씩 빼고 계산하여도 원래의 분산은 같다.
일반적으로 전체에서 임의로 몇 개가 사라져도 n-1로 나눈 분산이라면 기대값은 원래 분산과 같다. 시험점수의 분산 구할 때, 누군가 시험날 빠졌다고 해도 분산이 (정확히 말해 분산의 기대값이) 작아지지 않는다.
실무 TIP (엑셀 사용에 있어서 함수 사용 유의 사항)
# n으로 나누는 분산을 구하는데 사용하는 Excel 함수는 VARP()와 VAR.P()가 있다.
>
vars <- function(x) { var(x) *(length(x)-1) / length((x)) }
>
vars(1:5)
[1] 2
>
var(1:5)
[1] 2.5
표본을 사용해 표준편차를 구할 때 일반적으로 다음 식을 사용한다.
$$ s = \sqrt{s^2 } = \sqrt{ { 1 \over n-1 } \sum_{i=1}^n (X_i - \bar{X})^2 } $$
위의 공식은 R에 내장된 표준편차 함수 sd()를 사용한다.
>
x <- 1:5
>
sd(x)
[1] 1.581139
변이 계수는 측정 단위가 다르거나 평균이 크게 차이가 나는 두 자료의 산포를 비교하는 것으로 산식은 아래와 같다.
변이계수 : 모집단 = $ { σ \over μ } × 100 \% $ , 표본 = $ { s \over μ } × 100\% $
>
x <- 1:5
>
sd(x)/mean(x)
[1] 0.5270463
분산과 표준편차의 개념을 모르면 앞으로 있을 회귀 분석 / 딥러닝 등 여러가지 문제를 해결 하기 어렵다. 이 분은 꼭 집고 넘어가야 한다.
참고서적 : 누구나 통계 with R 길벗 출판사
통계학 개론 KNOU Press










댓글 없음:
댓글 쓰기