딥러닝을 그냥 시작 하면 매우 어려울 수도 있다. 왜냐 하면, 선형대수학이나, 통계학에 대한 기초 이론이 있어야 어느 정도 가능 하다. 이번에 하는 시간은 매우 적지만, 기초에 대한 부분을 우선 적으로 다룰 예정이다.
1. 딥러닝에 필요한 것들
우선 기호 부터 알아야 한다. 시그마( \( \sigma \) ) 무엇인지 모르는 분들이 많다. 이건 통계에서 사용 하는 용어이고, 이타(η) 라는 것이 무엇인지 잘모르는데, 이건 딥러닝에서 사용하는 용어이다. 아래는 목차를 나타낸 것이다.
수학 이론이 필수 적이다. 딥러닝을 배우면서, 수식을 간단하게 하기 위해 미분을 많이 사용 한다. 미분은 수식을 간단하게 하기 위한 증명용도로 사용한다. 딥러닝 할 때 꼭 필요한 부분만 하겠다.
통계학쪽으로 나가면, 평균, 분산, 표준 편차를 이해 하여야 만 회귀 분석을 할 수 있다. 딥러닝의 가장 기초적인 설명은 회귀분석에서 시작 한다. 그리고, 엔토로피가 있는데, 이것은 손실 함수 구하는데 가장 필수 적인 것이다. 선형대수학은 주로 행렬을 이야기 하는데, 다층 신경망을 다룰때 주로 사용될 것이다. 결국 다층 신경망은 여러개의 행렬로 이루어 진 것과 마찮가지이기 때문이다.
2. 수학 이론 (미분 )
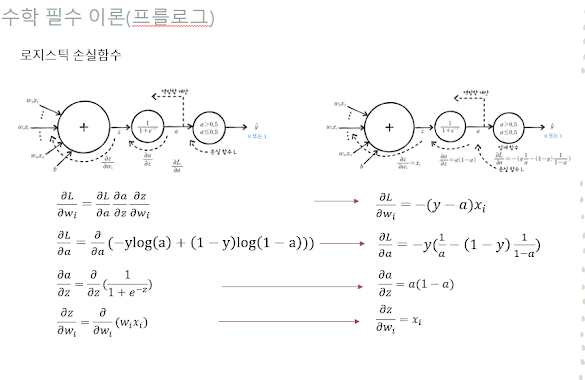
미분을 하는 이유는 아래 그림과 같이 로지스틱 손실 함수를 구할 때 사용 된다. 딥러닝은 손실 함수가 최소화 되는 시점까지 계산 하게 되는데, 물론 애폭을 많이 돌리면, 손실함수 최소점에 한계에 다다른다. 좌편의 그림과 같이 앤트로피, 시그모이드, 가중치를 체인룰에 의해 간단화 하는데 수학의 미분이 들어간다.
x에 대해서 미분을 하면 아래와 같이 제곱은 앞으로 나오고, 제곱 승은 1을 뺀다.
$$ {\operatorname{d}\over\operatorname{d}\!x} x^2 = 2x$$
log를 미분은 생각 보다 쉬운데, x 값이 분수로 되고 log 값이 없어진다.
$$ {\operatorname{d}\over\operatorname{d}\!x} log x ={ 1 \over x } $$
편미분은 2개의 다항식에서 한 가지만 미분 하는 것이다. 아래 예와 같이 x에 대하여 편미분을 한 결과가 나온다.
$$ f(x,y) = 2x^2y + x +1 $$
$$ {\partial\over\partial x} f(x,y) = 22xy = 4xy +1 $$
괄호가 들어 간 것을 미분을 하면 괄호 밖에 겉 미분과 속미분을 하여야 한다.
아래와 같이 ( \(x-y)^2 \) 식을 y에 대하여 편미분 하면?
$$ {\partial\over\partial y} (x - y)^2 = 2(x-y)x -1 = -2(x-y) $$
겉 미분과 속미분 2번을 하게 된다.
다변수 함수의 전미분은 아래와 같다. 우선 편미분을 한 다음에 더하면 된다.
\( z = x^2y^2 - 3x^2 +2 \) 를 미분하여라
$$ {\partial\over\partial x} = 2xy^2 -6x $$
$$ {\partial\over\partial y} = 2x^2y $$
$$ dz = f_x dx +f_y dy = (2xy^2 -6x)dx + (2x^2y)dy $$
함성 함수의 미분은 겉미분과 속미분을 하면 된다.
$$ dy/dx = (x^2 +1)^5 = 5(x^2 + 1)^4 × 2x = 10x(x^2 +1)^4 $$
아래 것은 log가 들어간 겉미분 하고 속 미분 하여야 하는데, 아래와 같이 변수를 치환 하는 테크닉을 써야 한다.
$$ dy/dx = log(x^2 +1), y = log \mu 이고 \mu = x^2 + 1일 때 = {1 \over \mu} \times 2x = { 2x \over( x^2+1)} $$
수학 분야에서 이것보다 더 많이 다루는 것은 의미가 없다. 앞으로 다루는 딥러닝은 제프리 힐튼 교수가 간단 한 수학으로 증명 하여 정리 하였다. 딥러닝의 대중화를 의해 최대한 쉽게 한것 같다. 수학 가지고 너무 머리 아파 할 필요가 없다. 우리는 간단한 수학만 알고 지나가면 된다. 너무나 많은 정보는 많은 혼란을 빠지게 하지 않는가? 꼭 필요한 정보만 담아서 가자.
댓글 없음:
댓글 쓰기